Interlocking Dodecagons

Çifte Minareli Medrese, Sivas/Turkey

interlocking dodecagons from caglar on Vimeo.

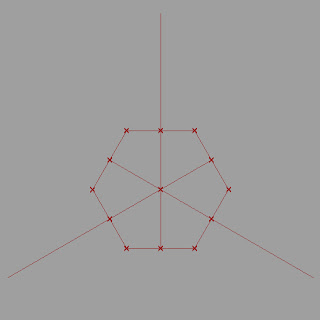
Setting up the rectangular grid, showing where the ratio Sx/Sy = 1/sqrt(3) comes from

If you want the dodecagons meet in their sides mid-points as in the original pattern , the proportions are as follows, where r is the radius of dodecagonal circumcircle and 2a is the size of one side. From the equation for the size of the inradius of a polygon;

inradius = r*cos(π/n)

Hence,

sqrt(r²-a²) = r*cos(π/12)

a = sqrt(r-(r*cos15))

We found the relationship between the side length and the radius of a dodecagon

We now need to define a grid in form of r and a. We know if we want the dodecagons to meet up in their sides midpoints distance between their centers would be  r+a*sqrt(2)

Which is,

r+(sqrt(r-(r*cos15))*sqrt(2))

This equals to the horizontal spacing of the grid (2x in the first picture).

ghx file

interlocking dodecagons.ghx

Hexagon Based Tesselation

Tomb of Izzettin Keykavus, Sivas/Turkey. 
We can barely see the pattern on the spandrels over the two side windows.

hexagons interlocking from caglar on Vimeo.

hexagon based tesselation point attractor from caglar on Vimeo.

The Concept

Take the mid points of a regular hexagon. Draw three axes as shown in the image(note the directions).

Move the mid-point pairs along these axes. You can as well move the three pair of points with different values. Any polygon you'll draw with this method will be seamlessly tileable. If you move all three starting points up to the hexagonal center, you'll get the Mitsubishi logo made up of three congruent rhombi which are made up of two equilateral triangles.

ghx file

hex tile.ghx

Triangle Centers, Simson Lines, Steiner Deltoid

Here are my Grasshopper methods to find some specific centers for a given triangle.


With the help of these centers, it's possible to draw Simson Lines and a Steiner Deltoid in Grasshopper.

The envelope of Simson Lines is the Steiner Deltoid.

Another way to build the deltoid is to draw two significant circles for a given triangle:
  
1.Feuerbach Circle(Nine-Point Circle): The circle that passes through nine significant points in a triangle

 Feuerbach Circle(Nine-Point Circle)

• The midpoint of each side of the triangle
• The foot of each altitude
• The midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).

     2. Steiner Circle: The circle whose center is the center of the Feuerbach Circle and whose radius is 1.5 times bigger than the circumcircle of the triangle.

When the Feuerbach Circle rolls around inside the Steiner Circle, a point on it traces the Steiner Deltoid.

Steiner Deltoid from caglar on Vimeo.

Definition has a method to find the Fermat Point of a triangle as well.

ghx file

triangle centers.ghx

Interlocking Octagons

interlocking octagons from caglar on Vimeo.

 

The spandrel of Muradiye Camii (Muradiye Mosque) in Bursa/Turkey.

Stone carving on the portal niche of Darüşşifa (hospital) in Divriği/Turkey.(Slightly different from the pattern in the animation)

  The pattern is based on four point stars in contact.

 

ghx file
interlocking octagons.ghx

pattern 5_4

5_4 from caglar on Vimeo.


This pattern is formed arraying five non-regular pentagons on four sides of a square. The tips of these four pentagons define another square which is the base of this tiling.

Playing with the variables, some sub-patterns appear. Looking carefully, you can as well see demiregular tiling of irregular decagons.

Another grid of interlocking octagons

Pattern with the point attractor

5_4 point attractor from caglar on Vimeo.

Mapping onto a sphere

5_4_hyperbolic from caglar on Vimeo.

ghx files
5_4
5_4 point attractor
5_4 hyperbolic

sixfold pattern on hex-grid

sixfold pattern on hex-grid from caglar on Vimeo.


A common hexagon based pattern found in beautiful tilings of Yeşil Cami (Green Mosque) in Bursa/Turkey. Equilateral triangles are arrayed around a regular hexagon.

 

ghx file

sixfoldpattern.ghx